Định thức

Để lại phản hồi Go to comments


(Bài này tiếp cận khái niệm định thức theo cách không chính quy nhằm tránh đề cập đến khái niệm phép thế, vốn là một khái niệm khá khó hiểu đối với những ngành ứng dụng, không chuyên Toán)

I. Các khái niệm cơ bản về định thức:

1. Định nghĩa định thức: Cho A = (a_{ij}) \in M_n(K) . Định thức ma trận A (ký hiệu det A hay |A|) là 1 giá trị được tính bởi công thức :

det(A) = |A| = a_{11}A_{11} + a_{12}.A_{12} + ... + a_{1n}.A_{1n}

trong đó: A_{ik} = (-1)^{i+k} .det(M_{ik}) , M_{ik} là ma trận vuông cấp n – 1 nhận được từ ma trận A bằng cách bỏ đi dòng thứ i và cột thứ k. Đại lượng A_{ik} được gọi là phần bù đại số của a_{ik}

2. Nhận xét:

- A = (a_{11}) \Rightarrow det A = a_{11}

- A \in M_2(K):

detA = { \left | \begin{array}{cc} a & b \\ c & d \\ \end{array} \right | } = a. (-1)^{1+1}.d + b.(-1)^{1+2}.c = ad - bc

- A \in M_3(K):

detA = { \left | \begin{array}{ccc} a & b & c \\ d & e & f \\ g & h & i \\ \end{array} \right | } = a.(-1)^{1+1}{ \left | \begin{array}{cc} e & f \\ h & i \\ \end{array} \right | } + b.(-1)^{1+2}{ \left | \begin{array}{cc} d & f \\ g & i \\ \end{array} \right |} \\+c(-1)^{1+3}{ \left | \begin{array}{cc} d & e \\ g & h \\ \end{array} \right|} = a(ei-hf) - b(di-fg)+c(dh-eg) \\ = (aei+bfg+cdh)-(ahf+bdi+ceg)

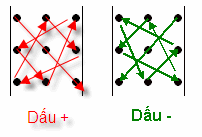
- Từ kết quả trên ta có quy tắc Sarrus để tính định thức cấp 3 như sau:

Quy tắc Sarrus
Quy tắc Sarrus

Ví dụ 1:

detA = { \left | \begin{array}{ccc} 2 & 3 & 1 \\ 3 & 1 & 4 \\ 1 & 2 & 2 \\ \end{array} \right | } = 2.1.2+3.2.1+3.4.1-1.1.1-2.4.2-3.3.2 \\ = -13

det1

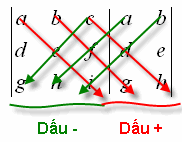
Từ quy tắc Sarrus trên, chúng ta còn có 1 quy tắc khác để tính nhanh định thức cấp 3:

- Ghép thêm cột thứ nhất và cột thứ hai vào bên phải định thức rồi nhân các phần tử trên các đường chéo như quy tắc thể hiện trên hình.


- A \in M_4(K) : không có quy tắc tính như định thức cấp 2 và định thức cấp 3, mà phải dùng định nghĩa để tính trực tiếp.

Ví dụ 2:

detA = { \left | \begin{array}{cccc} 1 & 3 & 0 & 2 \\ 4 & 1 & 2 &-1 \\ 3 & 1 & 0 & 2 \\ 2 & 3 & 3 & 5 \\ \end{array} \right | }

= 1.(-1)^{1+1}{ \left | \begin{array}{ccc} 1 & 2 & -1 \\ 1 & 0 & 2 \\ 3 & 3 & 5 \\ \end{array} \right | } + 3.(-1)^{1+2}{ \left | \begin{array}{ccc} 4 & 2 & -1 \\ 3 & 0 & 2 \\ 2 & 3 & 5 \\ \end{array} \right | } \\ +0.(-1)^{1+3}{ \left | \begin{array}{ccc} 4 & 1 & -1 \\ 3 & 1 & 2 \\ 2 & 3 & 5 \\ \end{array} \right | }+2.(-1)^{1+4}{ \left | \begin{array}{ccc} 4& 1 & 2 \\ 3 & 1 & 0 \\ 2 & 3 & 3 \\ \end{array} \right | }

(các bạn tính tiếp nhé)

3. Định lý:

Với ma trận vuông cấp n n \ge 2 ta có thể khai triển định thức của nó theo 1 dòng bất kỳ hoặc 1 cột bất kỳ theo các công thức sau:

- Theo dòng i: det(A) = |A| = a_{i1}A_{i1} + a_{i2}.A_{i2} + ... + a_{in}.A_{in}

- Theo cột j: det(A) = |A| = a_{1j}A_{1j} + a_{2j}.A_{2j} + ... + a_{nj}.A_{nj}

Với A_{ij} là phần bù đại số của phần tử a_{ij} được xác định như trên

Ví dụ: Tính

detA = { \left | \begin{array}{cccc} 2 & 2 & 3 & 4 \\ 2 & 0 & 1 & 0 \\ 4 & 0 & 3 & 2 \\ 4 & 1 & 2 & 5 \\ \end{array} \right | }

Nhận thấy dòng 2 có nhiều phần tử bằng 0 nhất nến ta khai triển theo dòng 2. Ta có:

detA = 2.(-1)^{2+1}{ \left | \begin{array}{ccc} 2 & 3 & 4 \\ 0 & 3 & 2 \\ 1 & 2 & 5 \\ \end{array} \right| } + 1.(-1)^{2+3}{ \left | \begin{array}{ccc} 2 & 2 & 4 \\ 4 & 0 & 2 \\ 4 & 1 & 5 \\ \end{array} \right| }

Vậy: detA = -2(30+6-12-8) - (16+16-40-4) =-20

Ngoài ra, ta cũng nhận thấy cột 2 có nhiều phần tử bằng 0 nhất nên ta cũng có thể khai triển theo dòng 2. Ta có:

detA = 2.(-1)^{2+1}{ \left | \begin{array}{ccc} 2 & 3 & 4 \\ 0 & 3 & 2 \\ 1 & 2 & 5 \\ \end{array} \right| } + 1.(-1)^{2+3}{ \left | \begin{array}{ccc} 2 & 2 & 4 \\ 4 & 0 & 2 \\ 4 & 1 & 5 \\ \end{array} \right| }

Vậy: detA = -2(30+8-8-20)+(4+24-16-12)=-20

Nhận xét: Giá trị của định thức của ma trận A là duy nhất.

Trang: 1 2

  1. Hieu
    22.09.2009 lúc 20:22 | #1
    Trả lời | Trích dẫn

    Thưa thầy em không hiểu chỗ “Nêu có một hàng là to hợp tuyến tính của hàng khác thì định thức bằng không”.
    Tổ hợp tuyến tính là gì ạ?

    • 2Bo02B
      22.09.2009 lúc 20:56 | #2
      Trả lời | Trích dẫn

      Cho ba số x, y, z. Ta nói z là tổ hợp tuyến tính của x, y nếu tồn tại 2 số m, n sao cho z = mx + ny.
      Cho 3 vecto x, y, z. Ta nói vecto z là tổ hợp tuyến tính của 2 vecto x, y nếu tồn tại 2 số m, n sao cho z = mx + ny.

  2. Hieu
    04.10.2009 lúc 20:12 | #3
    Trả lời | Trích dẫn

    vậy câu “nếu một hàng là tổ hợp tuyến tính của hàng khác” nghĩa là mỗi phần tử của hàng đó đều là tổ hợp tuyến tính của tất cả các hàng tử của hàng khác đúng không ạ?

    • 2Bo02B
      04.10.2009 lúc 20:43 | #4
      Trả lời | Trích dẫn

      d_i = [a_{i1} a_{i2} \ldots a_{in} ] là tổ hợp tuyến tính của dòng k: d_k = [a_{k1} a_{k2} \ldots a_{kn}] và dòng m d_k = [a_{k1} a_{k2} \ldots a_{kn}] nghĩa là tồn tại 2 số \lambda và \mu sao cho: a_{ij} = {\lambda}a_{kj} + {\mu}.a_{mj} ; \forall j = \overline{1;n}

  3. linh
    24.10.2009 lúc 20:30 | #5
    Trả lời | Trích dẫn

    Thầy ơi có cách tính nào về ma trận hình chữ nhật không thưa Thầy

    • 2Bo02B
      24.10.2009 lúc 21:45 | #6
      Trả lời | Trích dẫn

      Ý em là tính định thức của ma trận hình chữ nhật hả. Thầy chưa cập nhật nên ko biết có pp mới ko, chứ hiện tại, theo thầy biết, chưa có khái niệm định thức cho ma trận bất kỳ, chỉ có đối với ma trận vuông

  4. linh
    24.10.2009 lúc 20:42 | #7
    Trả lời | Trích dẫn

    Thầy ơi có phương pháp nào tách 1 ma trận A thành 2 ma trận B.C không Thầy?

  5. mot mi 90
    12.11.2009 lúc 20:59 | #8
    Trả lời | Trích dẫn

    moi nguoi giup mih bai tap nax nha
    tinh dih thuc sau:
    a b c d
    b a d c
    c d a b
    d c b a

    • 2Bo02B
      13.11.2009 lúc 22:27 | #9
      Trả lời | Trích dẫn

      Trên mỗi cột đều có chứa a, b, c, d nên đem các dòng cộng vào dòng 1, ta rút được nhân tử chung là a + b + c + d ra ngoài. Khi đó, dòng 1 xuất hiện 4 số 1. Dùng pp chuyển về ma trận tam giác. Em tính được định thức này.

  6. mot mi 90
    13.11.2009 lúc 08:52 | #10
    Trả lời | Trích dẫn

    thay oi thay co the phan biet giup e phan biet he sinh va span duoc ko a?
    phan khong gian vec to va phan ma tran,dinh thuc ,he phuong trinh co moi lien he voi nhau nhu the nao?

    • 2Bo02B
      13.11.2009 lúc 22:04 | #11
      Trả lời | Trích dẫn

      Trong kgvt V, cho một hệ M gồm hữu hạn vecto. Khi đó, tập hợp tất cả các tổ hợp tuyến tính của hệ M là không gian con của V và gọi là bao tuyến tính (span) của M (hay không gian con sinh bởi hệ M). ký hiệu spanM =
      là kgc nhỏ nhất trong các kgc của V chứa M.
      Khi V = thì ta bảo M là 1 hệ sinh của V. Nghĩa là, nếu bao tuyến tính sinh ra toàn bộ không gian V thì M được gọi là hệ sinh.
      Ví dụ: trong kgvt R^3 , xét hệ vecto M = {(1,0,1);(1,1,0)} thì spanM = \{a(1,0,1)+b(1,1,0)\} = \{(a+b,b,a) \}
      M không là hệ sinh ra R^3. Tuy nhiên với hệ các vecto có dạng (a+b,a,b) thì M chính là hệ sinh.

  7. mot mi 90
    14.11.2009 lúc 09:58 | #12
    Trả lời | Trích dẫn

    Thầy có thể giúp em bài này không ạ? Tính định thức sau:
    \left|\begin{array}{ccc} a+b & ab & a^2+b^2 \\ b+c & bc & b^2+c^2 \\ c+a & ca & c^2 + a^2 \\ \end{array} \right|
    Không khai triển định thức mà dùng tính chất của định thức để chúng minh:
    \left|\begin{array}{ccc} 1 & a & a^3 \\ 1 & b & b^3 \\ 1 & c & c^3 \\ \end{array} \right| = (a+b+c) \left|\begin{array}{ccc} 1 & a & a^2 \\ 1 & b & b^2 \\ 1 & c & c^2 \\ \end{array} \right|

Comment pages
  1. No trackbacks yet.