Maths 4 Physics & more…
1. Các kết quả:
Biểu thức Toán học:
(1)
được gọi là chuỗi Fourier nếu (1) hội tụ.
1.1 Định nghĩa. Một đa thức Fourier là biểu thức có dạng:
Các hệ số a0, ai và bi, i = 1,2,…, n, được gọi là hệ số của Fn(x).
Đa thức Fourier là hàm tuần hoàn với chu kỳ 2π. Sử dụng các công thức lượng giác cơ bản ta có:
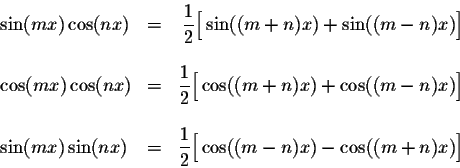
Chúng ta có thể chứng minh dễ dàng các công thức sau:
(1) Với n ≥ 0, ta có:
và
(2) Với mọi m , n ta có:
(3) Với n ≠ m, ta có:
và
(4) Với n ≥ 1, ta có:
và
Sử dụng các công thức trên, chúng ta có kết quả sau:
1.2 Định lý: Cho
Ta có:
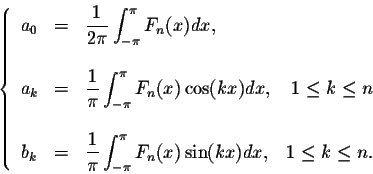
Định lý trên giúp ta có thể tìm được hệ số Fourier của các hàm tuần hoàn với chu kỳ T = 2π.
2. Khai triển hàm số thành chuỗi Fourier:
Định nghĩa. Cho f(x) là hàm tuần hoàn với chu kỳ T = 2π và khả tích trên đoạn [- π ; π]. Đặt:
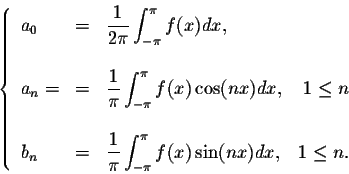
Khi đó, chuỗi lượng giác:
được gọi là khai triển Fourier của hàm số f(x) tương ứng. Ký hiệu:


Thầy giúp e khai triển fourier f(x)=x^2 x=(0;pi) và f(x)=x(pi-x) x=(0-pi)
ThíchThích
Posted by Minh Phạm | 03/07/2017, 18:25Thầy giúp e 2 bài này với.
Khai triển ham f(x) tuân hoàn chu ky 2pi thành chuỗi Florida.
a. f(x)=sinax, -pi<x<pi, a#k
b. f(x)=(pin-x)/2, 0<x<2.
ThíchThích
Posted by Khoa | 27/01/2015, 10:54khai triển chuỗi Furie của hàm F(x)=x^2 (-pi,pi)
thầy giúp em bài này với! e cảm ơn thầy nhiều!!
ThíchThích
Posted by bmthanh1181995 | 19/02/2014, 11:45khai triển thành chuỗi fourier chu kì 2pi;
f(x)=|X^3| trên [-pi;pi];
thầy hướng dẫn em cách làm bai này với!!! thầy có thể vẽ đồ thị bài này cho em được ko ạ?? em cám ơn thây!!!
ThíchThích
Posted by nho_pro | 23/05/2011, 22:03Em phá bỏ trị tuyệt đối, khi đó:
![f(x) = \left\{\begin{array}{cc} -x^3 & ; [-\pi;0] \\ x^3 & ; [0; \pi] \\ \end{array} \right.](https://s0.wp.com/latex.php?latex=f%28x%29+%3D+%5Cleft%5C%7B%5Cbegin%7Barray%7D%7Bcc%7D+-x%5E3+%26+%3B+%5B-%5Cpi%3B0%5D+%5C%5C+x%5E3+%26+%3B+%5B0%3B+%5Cpi%5D+%5C%5C+%5Cend%7Barray%7D+%5Cright.+&bg=ffffff&fg=333333&s=0&c=20201002)
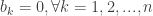
Sau đó, ráp công thức hàm f(x) vào công thức khai triển.
Ngoài ra, nếu em chú ý đến tính chất chẵn, lẻ của hàm f(x) thì em sẽ có
ThíchThích
Posted by 2Bo02B | 26/05/2011, 22:27E cảm ơn bài giảng của thầy. Nhờ nó mà e đã hiểu!!!!! Cảm ơn thầy rất nhiều!
ThíchThích
Posted by nguyen thi anh tuyet | 13/01/2011, 11:17Hello Sir,
Thanks for uploading the Fourier Problem set.
I was going through the problem set – thunhan.files.wordpress.com/2007/10/problemsfourier.pdf.
In the following problem Problem 1 (g) I think the asnwer is 2*pi.
Here is my understanding.
x(t) = 5*Cos(3*x) + 2*Cos(2*x)
Fundamental Period of 5*Cos(3*x) is T1 = 2*pi/3.
Fundamental Period of 2*Cos(2*x) is T2 = pi
Hence the Fundamental Period of x(t) is LCM (T1, T2) = T1*m = T2*k.
where m and k are smallest possible integers so as to make LCM a integer.
(2*pi/3)*m = pi*k
Hence m is 3 and k is 2.
LCM is 2*pi.
Logically also period of 3 fundamental wave of 1st wave = period of 2 fundamentel wave of 2nd wave.
—
– Harish
Be exhilarated forever
ThíchThích
Posted by harish kalghatgi | 04/09/2010, 10:38Thầy ơi, nếu khai triển hàm f(x) thành chuỗi Fourier trên (0, 2Pi) thì em phải làm thế nào ạ?
ThíchThích
Posted by Anh Tran | 02/11/2009, 18:13