Maths 4 Physics & more…
Shortlink: http://wp.me/P8gtr-7p
KEYWORD: Integrals involving roots, Euler substitution
1. Các tích phân cơ bản:NEW UPDATE
1.
2.
3.
4.
2. Tích phân dạng:
Gọi s là mẫu số chung của
Đặt: để đưa về tích phân hữu tỉ.
Ví dụ 2.1: Tính
Do trong biểu thức tính tích phân có chứa nên ta đặt:
Khi đó:
Nên:
Áp dụng dạng 3 của tích phân phân thức hữu tỉ ta có:
Hay:
Do đó:
Vậy:
Ví dụ 2.2: Tính
Đặt khi đó
và:
3. Tích phân nhị thức vi phân:
Tích phân chỉ có nguyên hàm nếu rơi vào 1 trong 3 trường hợp sau:
1.
. Đặt
. Với s là mẫu số chung của m và n.
2.
. Đặt
, với k là mẫu số của p.
3.
. Dùng phép thế
, với k là mẫu số của p.
Ví dụ 3.1: Tính
Ta có:
Khi đó:
Vậy tích phân thuộc dạng 2 nên đặt:
Suy ra:
Thế vào tích phân ta có:
Vậy:
Do đó:
Ví dụ 3.2: Tính
Do nên tích phân trở về tích phân dạng 2. Do đó, ta đặt:
Khi đó:
Tới đây, tích phân đã trở về dạng phân thức hữu tỉ. Tuy nhiên, nếu làm máy móc, ta phải phân tích phân thức này thành 10 phân thức hữu tỉ thật sự. Do đó, ta biến đổi tử số như sau:
Vậy kết quả là:
Ví dụ 3.3: Tính
Ta có:
Suy ra:
Vậy, ta đặt:
Để việc thế biến vào tích phân đơn giản, ta biến đổi tích phân để xuất hiện biểu thức trước. Ta có:
Xét ta có:
(*)
Thế vào (*) ta có:


thầy ơi thầy giúp em làm 2 bài này với ạ
nguyên hàm dx / x+ căn bậc hai (x^2+x+1)
nguyên hàm dx/(1+2 căn x+ căn bậc 3 của x)
em cám ơn ạ !
ThíchThích
Posted by Huyen Pham | 10/05/2013, 22:51Thầy ơi cho e hỏi những loại tích phân không có nguyên hàm thì hướng xử lí như thế nào
ThíchThích
Posted by hùng | 18/06/2012, 09:58thầy ơi! ở ví dụ 3 phần tích phân nhị thức vi phân, thầy có nhầm 1 chỗ ở đoạn cuối: -2x^-3dx = 2tdt x^-3dx = -tdt … nhưng bên dưới lại bị thiếu mất dấu trừ nên kết quả cuối bị ngược dấu, thay vì kết quả có dấu (-) thì lại không có!
ThíchThích
Posted by mr_angel9x | 04/12/2011, 16:02Xin thầy giải cho em bài tich phân này:
tích phân từ 0 đến duong7 vô cùng hàm (x^2 + 1)(x^2 – 3x – 1)/(x^6 + 4x^3 – 1)
ThíchThích
Posted by nguyenhai | 24/09/2011, 20:29Thầy ơi trên này là tất cả các phương pháp tính tích phân hàm vô tỉ phải không ạ.
Cám ơn thầy . Thầy cho em hỏi còn phần lượng giác và hữu tỉ co trên này không thầy. Em muốn cop về để hệ thống kiến thức luôn một thể.
ThíchThích
Posted by Hoàng Phương Nguyên | 24/01/2011, 21:04hay quá ạ cảm ơn thầy
ThíchThích
Posted by Nguyên Chương | 20/12/2010, 16:25thầy ơi giúp em bài này với:

ThíchThích
Posted by Nguyên Chương | 20/12/2010, 00:11Tích phân này có lũy thừa của sinx và cosx đều là lũy thừa bậc chẵn nên ta đặt:
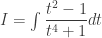
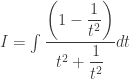

Khi đó:
Em có thể tính tích phân này theo phương pháp tích phân hữu tỉ. Tuy vậy, tích phân ở đây có dạng trùng phương, do đó, em có thể tính như sau:
Đặt
ThíchThích
Posted by 2Bo02B | 20/12/2010, 14:48Nhờ thầy giải dùm bài tích phân đi từ 1 đền 2 của hàm số x^x
ThíchThích
Posted by Lê Hữu Nhân | 13/01/2010, 19:48Your blog keeps getting better and better! Your older articles are not as good as newer ones you have a lot more creativity and originality now keep it up!
ThíchThích
Posted by Britnifreeman | 05/01/2010, 16:27có ai tính dùm tích phân từ o đến 1 của (X^4+X^2+1)/(X^6+1) với làm được cảm ơn trước nha
ThíchThích
Posted by huy | 24/06/2009, 20:14