Nhân dịp năm học mới, M4Ps xin giới thiệu đến các bạn những hình ảnh tuyệt vời của Toán học. Những hình ảnh này là 1 minh chứng rõ ràng nhất cho việc khẳng định Toán học không phải là môn học khô khan, mà ngược lại nó chứa đựng những vẻ đẹp của cuộc sống.
Đây là đồ thị của những đường cong tham số, và đường cong trong tọa độ cực cũng như những đường cong trong không gian, chúng được tạo thành từ những đường cong quen thuộc khi chúng ta cho những giá trị của tham số thay đổi. Ví dụ như: đường lemniscarte ,
, đường Cardioid hay :
Những hình ảnh này được M4Ps thực hiện bằng phần mềm vẽ đồ thị 2.25 của tác giả Hà Hoàng Phương và phần mềm Maple.
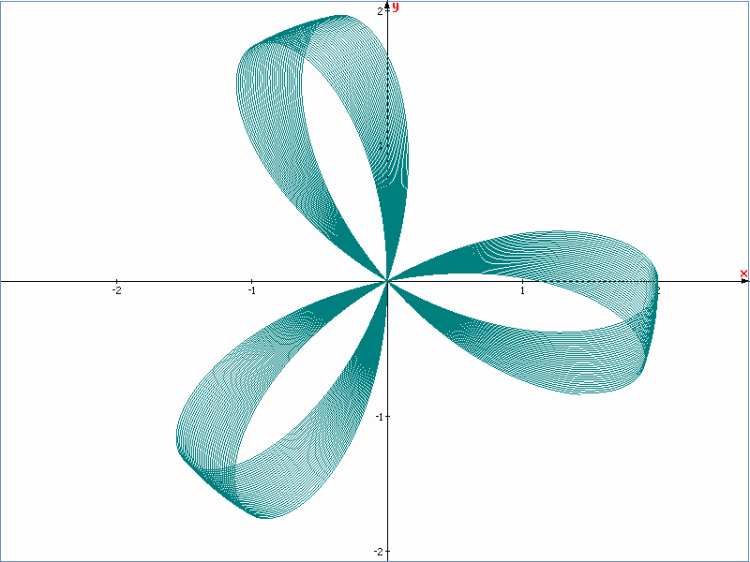
Hình nơ đôi 3 cánh – Đồ thị hàm số
Số 8 may mắn – Đồ thị hàm
Với phương trình trên, ta chỉ cần thay đổi một chút sẽ có những hình ảnh thú vị khác:
Tiếp theo là một số dạng đồ thị của đường cong:
Phương trình đường cong: x(t) = 3cos(0.4t)+2sin(0.6t) ; y(t) = 3sin(0.4t)+2cos(0.6t).
Phương trình con bướm:
Có thể bạn sẽ nghĩ rằng làm sao mà vẽ được mặt người phải không? Có thể bạn sẽ phải suy nghĩ lại sau khi nhìn thấy đồ thị của hàm số . Đây là đường cong trong tọa độ cực mà M4Ps đã mày mò tạo ra suốt buổi chiều nay, và để cho giống mặt người, M4Ps bổ sung thêm con mắt và cái miệng. Bạn xem thử giống không nhé!















thầy ơi phần mềm vẽ đồ thị thầy sử dụng có tên gì vậy ạ?
ThíchThích
Posted by Duong | 30/09/2012, 20:53theo mình biết thì có thể dùng function grapher 2011 (phần mềm thuần việt) hoặc dùng maple 16
ThíchThích
Posted by đạt | 25/10/2012, 10:35môn toán thật là kỳ diệu
ThíchThích
Posted by nhat long | 01/02/2012, 22:22Thật là đẹp.Lại có thêm một lí do nữa để yêu môn toán rồi!
ThíchThích
Posted by xuanlan | 05/12/2011, 18:28Pythagorean theorem 😮 😮 😮
ThíchThích
Posted by Đức Anh | 09/11/2011, 00:24Tuyệt thật! Đúng là vẻ đạp của Toán học
ThíchThích
Posted by sunnyflower | 06/11/2011, 19:01phương trình cánh bướm làm mình nhớ tới Nhân Hút Lorenz quá, cũng có hình cánh bướm nhưng trong không gian 3 chiều,
tác giả kỳ công quá, thanks đã chia sẻ!
ThíchThích
Posted by nguyenchithang | 05/11/2011, 20:42Làm thế nào mà thầy tìm ra được những phương trình như vậy?
ThíchThích
Posted by Tiến | 02/11/2011, 12:52Ngoài phương trình con bướm (phát hiện khi đọc tài liệu) thì các pt còn lại là do thay đổi các thông số từ những pt cơ bản (Lemniscartes, Cardioid) như đã đề cập ở đầu bài đó em. Nhờ phần mềm vẽ đồ thị, kh thay đổi, thấy đồ thị nào hay hay thì giữ lại.
ThíchThích
Posted by 2Bo02B | 02/11/2011, 21:32thật tuyệt vời, có vẻ như tạo hóa hình thể của vạn vật là một sự tính toán toán học hoàn hảo !!!
ThíchThích
Posted by Thịnh | 28/10/2011, 13:37hay qua. từ toán đồ thị hàm số ma có thể vẽ ra vô số hình ành khác nhau
ThíchThích
Posted by haidangwy | 26/09/2011, 18:19Thưa thầy, thật sự rất nghệ thuật.
ThíchThích
Posted by (¯`•Oºo.OßơO.oºO•´¯) | 09/09/2011, 22:26đẹp quá thầy ơi. :d
không thể chê vào đâu dc.
ThíchThích
Posted by Liên Duy | 07/09/2011, 18:57tuyệt vời thầy Nhân ơi, nhưng mà mấy cái phường trình này, ngoài đẹp mắt ra còn có công dụng gì không??
ThíchThích
Posted by caman006 | 04/09/2011, 23:08