Shortlink: http://wp.me/P8gtr-I2

Nội dung bài viết này không đi sâu vào các vấn đề lý thuyết của bài toán mà sẽ bàn luận các phương pháp để giải quyết các bài tích phân 2 lớp rơi vào những trường hợp phải chuyển qua tọa độ cực hoặc đổi biến. Vì vậy, các bạn nên xem các giáo trình liên quan để nắm rõ cơ sở lý thuyết của bài toán.

1. Mối liên hệ giữa tích phân 2 lớp trong tọa độ Decarster (Đề- các) vuông góc (Oxy) và tọa độ cực:

(1)

Chú ý:

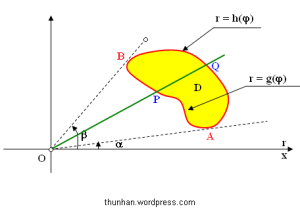1. Nếu miền lấy tích phân D giới hạn bởi 2 tia xuất phát từ cực: tiếp xúc với biên của miền D tại A và B và đoạn đường cong APB có phương trình , đoạn đường cong AQB có phương trình: thì (1) được tính như  sau:

(2)

2. Nếu gốc O nằm trong miền D và mọi tia xuất phát từ O đều cắt biên của miền HD tại 1 điểm có bán kính vec tơ là thì:

3. Trong tọa độ cực để tích tích phân 2 lớp thường tính tích phân theo r trước.

2. Phương pháp xác định cận:

Bước 1: Nhập môn. Cần nằm lòng 4 điều quan trọng sau:

1. Bài toán nào thì chuyển sang tọa độ cực được?

Mọi bài toán đều có thể chuyển qua tọa độ cực được. Tuy nhiên, ta chỉ nên đổi để biến miền D từ phức tạp thành đơn giản. Bài nào tính dễ dàng trong tọa độ vuông góc thì bạn cứ tính toán bình thường. Ta chỉ đổi sang hệ tọa độ cực khi:

– Hàm dưới dấu tích phân có chứa , đồng thời miền D giới hạn bởi các đường thẳng đi qua O.

– Miền lấy tích phân D là hình tròn, hình tròn lệch, giới hạn của hai hình tròn, hoặc đường cong có chứa

2. Với những miền lấy tích phân nào mà bạn có thể vẽ hình được thì nên vẽ ra vì như thế sẽ dễ dàng xác định cận lấy tích phân hơn.

3. Trước khi chuyển cận, bạn nên chú ý xem miền D và hàm lấy tích phân có tính chất đối xứng không? Điều này sẽ giúp ta thu hẹp miền lấy tích phân:

1. Nếu miền D đối xứng qua Ox và f(x;y) = f(x;-y) thì:

(với D1 là phần của D ứng với y > 0)

Nếu miền D đối xứng qua Ox và f(x;y) = -f(x;-y) thì:

2. Tương tự, nếu miền D đối xứng qua Oy và f(x;y) = f(-x;y) thì:

(với D’ là phần của D ứng với x > 0)

Nếu miền D đối xứng qua Ox và f(x;y) = -f(-x;y) thì:

3. Nếu miền D là miền đối xứng qua Ox và Oy và f(x;y) = f(-x;y) = f(x;-y) = f(-x;-y) thì:

(với D* là phần của D nằm trong góc phần tư thứ nhất)

4. Để xác định chính xác cận tích phân, ta phải xét trong tọa độ cực thông thường, không xét trong tọa độ cực mở rộng. Nghĩa là: , tức r dương, góc quay chỉ xét trong 1 vòng đường tròn lượng giác.

Bước 2: Xuất chiêu. Phương pháp xác định cận:

Cách 1:  xác định cận bằng phương pháp hình học.

– Vẽ miền lấy tích phân D.

– Xác định 2 tia tiếp xúc với biên miền D.  Nghĩa là, tìm 2 phương trình đường thẳng tiếp xúc với đường cong  (C) giới hạn miền D lần lượt tại A, B.

– Vẽ bất kỳ 1 tia nằm giữa cắt biên D tại 2 điểm P, Q.  Xác định phương trình của  cung APB và AQB bằng cách chuyển đường cong (C) qua tọa độ cực. Tìm biểu thức xác định của r. Biểu thức nào có giá trị r nhỏ hơn, đó chính là phương trình của cung APB: ,  còn lại là phương trình của cung AQB: .

Nếu O thuộc miền D, hoặc trên biên của miền D thì cận dưới

Khi đó: cận tích phân sẽ là