Khái niệm về ma trận

I. Các định nghĩa về ma trận:

1. Định nghĩa 1.1:

Một ma trận A loại (cấp) m x n trên trường K (K – là trường thực R, hoặc phức C) là một bảng chữ nhật gồm m x n phần tử trong K được viết thành m dòng và n cột như sau:

$A = \left ( {\begin{array}{ccccc} a_{11} & a_{12} & a_{13} & \cdots & a_{1n} \\ a_{21} & a_{22} & a_{23} & \cdots & a_{2n} \\ a_{31} & a_{32} & a_{33} & \cdots & a_{3n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & a_{m3} & \cdots & a_{mn} \\ \end{array}} \right )$

Trong đó $a_{ij} \in K$ là phần tử ở vị trí dòng i, cột j của A. Đôi khi A được viết ngắn gọn là $A = (a_{ij})_{mxn}$ hay $(A)_{mxn}$

Các ma trận thường được ký hiệu bởi A, B, C và tập hợp tất cả các ma trận loại m x n trên trường K được ký hiệu bởi M_{m x n}(K)

Ví dụ 1.1: $A = \left( {\begin{array}{ccc} 0 & -1 & 1 \\ 1 & 2 & 3 \\ \end{array}} \right )$ là ma trận cấp 2 x 3. $B = \left( {\begin{array}{cc} -2 & 1 \\ 1 & 2 \\ 0 & 3 \\ \end{array}} \right )$ là ma trận cấp 3 x 2.

Ví dụ 1.2: Viết ma trận cấp 4 x 4 biết: $a_{ij} = i^2 - j^2 , \forall i,j = 1, ... , 4$

Nhận xét:

– Ma trận A có thể xác định trực tiếp bằng cách liệt kê các phần tử, cũng có thể được xác định theo công thức tổng quát.

– Ma trận không cấp m x n (ma trận zero), ký hiệu 0_mxn là ma trận mà mọi phần tử đều bằng 0.

– Nếu m = n thì A được gọi là ma trận vuông cấp n trên K. Tập hợp tất cả các ma trận vuông cấp n trên K được ký hiệu là M_n(K)

– Ma trận cấp 1 x n được gọi là ma trận hàng; ma trận cấp m x 1 được gọi là ma trận cột

– Nếu A là ma trận vuông cấp n, thì đường chứa các phần tử a₁₁, a₂₂, a₃₃,…, a_nn được gọi là đường chéo chính của A.

2. Định nghĩa 1.2: Cho $A = (a_{ij}) \in M_n(K)$ . Khi đó:

– Nếu $a_{ij} = 0 , \forall i \ne j$ (nghĩa là tất cả các phần tử bên ngoài đường chéo chính của A đều bằng 0) thì ta nói A là ma trận đường chéo.

– Ta thường dùng ký hiệu diag(a₁, a₂,…, a_n) để chỉ một ma trận đường chéo cấp n có các phần tử trên đường chéo lần lượt là a₁, a₂, …, a_n

– Ma trận chéo có $a_{ii} = 1 , \forall i$ (nghĩa là các phần tử trên đường chéo chính đều bằng 1) được gọi là ma trận đơn vị. Ký hiệu: I_n

– Một ma trận đường chéo với tất cả các phần tử trên đường chéo chính đều bằng nhau được gọi là ma trận vô hướng.

– Nếu $a_{ij} = 0 , \forall i > j$ (nghĩa là tất cả các phần tử nằm bên dưới đường chéo chính của A đều bằng 0) thì ta nói A là ma trận tam giác trên.

– Nếu $a_{ij} = 0 , \forall i < j$ (nghĩa là tất cả các phần tử nằm bên trên đường chéo chính của A đều bằng 0) thì ta nói A là ma trận tam giác dưới.

– Ma trận tam giác trên hay tam giác dưới được gọi chung là ma trận tam giác.

II. Các phép toán trên ma trận:

1. Định nghĩa 2.1 (hai ma trận bằng nhau):

Cho $A = (a_{ij}), B = (b_{ij}) \in M_{mxn}(K)$ .

Ta nói A = B khi và chỉ khi: $a_{ij} = b_{ij} , \forall i, j$

Ví dụ: Với $A = \left ( {\begin{array}{ccc} 1 & 2 & 3 \\ a & b & c \\ \end{array}} \right ) ; B = \left ( {\begin{array}{ccc} d & e & f \\ 4 & 5 & 6 \\ \end{array}} \right )$ Thì $A = B \leftrightarrow a = 4 , b = 5 , c = 6 , d = 1, e = 2, f = 3$

Hai ma trận $A = \left ( {\begin{array}{cc} 1 & 2 \\ 3 & 4 \\ \end{array}} \right ) ; B = \left ( {\begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ \end{array}} \right )$ không thể bằng nhau do không cùng cấp.

2. Định nghĩa 2.2 (Ma trận chuyển vị):

Cho $A = (a_{ij}) \in M_{mxn}(K)$ . Ta nói:

$B = (b_{ij}) \in M_{mxn}(K)$ là chuyển vị của A (ký hiệu B = A^T) nếu:

$a_{ij} = b_{ij} , \forall i, j$

Ví dụ: Nếu $A = \left ( {\begin{array}{ccc} 1 & 3 & 5 \\ 2 & 4 & 6 \\ \end{array}} \right )$ thì ${A^T} = \left ( {\begin{array}{cc} 1 & 2 \\ 3 & 4 \\ 5 & 6 \\ \end{array}} \right )$

3. Tính chất 2.1:

Cho $A, B \in M_{mxn}(K)$ . Khi đó:

1. $(A^T)^T = A$

2. $A^T = B^T \Leftrightarrow A = B$

Ghi chú:

Cho $A \in M_n(K)$ . Khi đó, nếu A^T = A thì ta nói A là ma trận đối xứng; nếu A^T= – A thì ta nói A là ma trận phản xứng.

Ví dụ: $A = \left ( {\begin{array}{ccc} 1 & 2 & 3 \\ 2 & 4 & 5 \\ 3 & 5 & 0 \\ \end{array}} \right )$ là ma trận đối xứng. $B = \left ( {\begin{array}{ccc} 0 & 1 & {-2} \\ {-1} & 0 & 3 \\ 2 & {-3} & 0 \\ \end{array}} \right )$ là ma trận phản xứng.

Nhận xét: Nếu B là ma trận phản xứng thì các phần tử trên đường chéo chính của B đều bằng 0.

4. Phép nhân một số với một ma trận:

Cho $A \in M_{mxn}(K) , a \in K$ Ta gọi tích a và A (ký hiệu aA) là một ma trận $C = (c_{ij}) \in M_{mxn}(K)$ được xác định bởi: $c_{ij} = a.a_{ij}$

– Nếu a = -1 thì ta ký hiệu (-1).A bởi -A và gọi là ma trận đối của A.
5. Cộng hai ma trận:

Cho $A, B \in M_{mxn}(K)$

Ta gọi tổng của A và B (A + B) là một ma trận $C = (c_{ij}) \in M_{mxn}(K)$ được xác định bởi: $c_{ij} = a_{ij} + b_{ij}$

Tổng của A + (-B) được ký hiệu bởi A – B và gọi là hiệu của ma trận A và B.
6. Tính chất 2.2:

Cho $A \in M_{mxn}(K) ; \alpha , \beta \in K$ . Ta có: (ab).A = a.(bA); (aA)^T = a.(A^T)

7. Ví dụ: Xác định các giá trị của x, y sao cho:

8. Định lý 2.1:

Cho $A \in M_{mxn}(K) ; \alpha , \beta \in K$ . Khi đó:

1.Tổng hai ma trận có tính giao hoán: A + B = B + A

2.Tổng hai ma trận có tính kết hợp: A + (B + C) = (A + B) + C

3.Tồn tại ma trận 0_mxn sao cho: A + 0 = 0 + A = A

4. Tồn tại ma trận đối của A sao cho: A + (- A) = (- A) + A = 0

5.Phép nhân vô hướng có tính phân phối: α(A+B) = αA + αB ;(α +β)A = αA + βA

6.Chuyển vị của tổng bằng tổng các chuyển vị:(A + B)^T = A^T + B^T

Thảo luận

40 bình luận về “Khái niệm về ma trận”

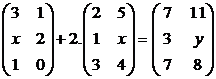
giúp e chứng minh A.B=0 => A=O hoặc B=0 là đúng hay sai ?

ThíchThích

Posted by duy | 16/07/2016, 11:18

Reply to this comment
Thầy ơi cho em hỏi. Nếu đề bài hỏi là 2 ma trạn A và B có đồng dạng hay không? Thì em có thể giải quyết dạng bài này như thế nào ạ

ThíchThích

Posted by khuongbka | 18/01/2015, 09:54

Reply to this comment
cho em hỏi ma trận đối xứng có bao nhiêu cặp số bằng nhau

ThíchThích

Posted by ngọc bích | 10/01/2014, 15:59

Reply to this comment
- Ma trận đối xứng có tính chất $a_{ij} = a_{ji} (i \neq j)$ Nên nếu xét ma trận vuông cấp n thì em có thể tính toán bằng cách liệt kê:
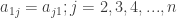  – Với i = 1 thì $a_{1j} = a_{j1}; j = 2, 3, 4,..., n$ có n – 1 cặp số giống nhau
  – Với i = 2 thì $a_{2j} = a_{j2}; j = 3, 4,..., n$ có n – 2 cặp số
  ……
  Từ đó, em sẽ có kết quả: 1 + 2 + 3 + …. + (n-1)
  
  ThíchThích
  
  Posted by 2Bo02B | 20/03/2014, 15:30
  
  Reply to this comment
Xin thầy cho e hỏi, trong 1 ma trận vuông có mấy đường chéo chính ạ? Ở phần lý thuyết trên thầy nói đến các phần tử a[i,j] mà i=j thì sẽ nằm trên đường chéo chính, còn các phần tử a[i,j] mà i+j=n+1 thì cũng nằm trên đường chéo của ma trận vuông đó, nhưng đường chéo đó gọi là đường chéo chính hay đường chéo phụ vậy? E xin cảm ơn thầy.

ThíchThích

Posted by Nguyễn Hằng | 09/10/2012, 21:16

Reply to this comment
Thầy ơi cho e hỏi làm sao để nhân 1 chuỗi ma trận với nhau ạ? cách tính thế nào ạ?

ThíchThích

Posted by Bao Nghi | 23/07/2012, 22:21

Reply to this comment
em cám ơn thầy ạ ^^

ThíchThích

Posted by Bunie | 21/02/2012, 20:31

Reply to this comment
thầy ơi cho em hỏi tính lũy thừa của ma trận cấp n thì tính thế nào vd: lũy thừa 14 lần chả hạn của ma trận A cấp 3 chả hạn ?

ThíchThích

Posted by Phuong | 29/01/2012, 09:05

Reply to this comment
Đề ra là : tính |A|. Tìm điều kiện của m để |A| nghịch đảo?

ThíchThích

Posted by Trần Thái | 02/01/2012, 20:27

Reply to this comment
cho em hỏi ma trận nghịch đảo của ma trận có 1 phần tử là gì ạ:(

ThíchThích

Posted by huynh | 16/12/2011, 17:03

Reply to this comment
Thưa Thầy!các phần tử trên đường chéo chính có phần tử bằng không thì có được gọi là ma trận tam giác không?

ThíchĐã thích bởi 1 người

Posted by Huyền | 06/11/2011, 23:28

Reply to this comment
- Em xem lại định nghĩa ma trận bậc thang nhé. Ma trận bậc thang không phụ thuộc vào việc các phần tử trên đường chéo chính bằng 0 hay khác 0. Vì:
  – Thứ nhất, một ma trận cấp mxn bất kỳ luôn có dạng bậc thang, chứ không cần phải ma trận vuông (ma trận có đường chéo chính)
  – Thứ hai, nếu là ma trận vuông vẫn tồn tại ma trận bậc thang mà có các phần tử trên đường chéo chính bằng 0. Ví dụ:
  $\left[\begin{array}{cccc} 0 & 1 & 2 & 3 \\ 0 & 0 & 1 & 2 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ \end{array} \right]$
  
  ThíchThích
  
  Posted by 2Bo02B | 07/11/2011, 13:19
  
  Reply to this comment
Thưa thầy,cho em hỏi là chúng ta có thể dùng như mặc định rằng một ma trận vuông A lũy thừa 0 thì bằng ma trận đơn vị E ko ạ ? Và E lũy thưa n luôn = E nữa ? em xin cám ơn

ThíchThích

Posted by Ân | 02/10/2011, 18:28

Reply to this comment
thưa thầy tại sao em ko thấy phép nhân 1 dòng với một số trong ma trận.
Mà em thấy khi dùng biến đổi ma trận về ma trận đơn vị lại đc dùng phép tính trên???

ThíchThích

Posted by thiện | 09/03/2011, 16:22

Reply to this comment
- Phép biến đổi sơ cấp là phép biến đổi đưa ma trận về một ma trận mới có tính chất tương đương với nó. Dĩ nhiên, 2 ma trận chỉ tương đương chứ không phải ma trận này bằng bao nhiêu lần ma trận kia nên nó không phải là một phép toán trên ma trận. Phép biến đổi xuất hiện dựa trên quá trình giải hệ phương trình: đổi chỗ 2 pt cho nhau, nhân 1 pt với một hằng số.
  Do đó, em cần phân biệt các phép toán trên ma trận với các phép biến đổi:
  – Phép toán: cộng trừ hai ma trận cùng cấp, nhân 2 ma trận; lũy thừa của 1 ma trận vuông, nhân ma trận với 1 hằng số….
  – Phép biến đổi: phép chuyển vị; 3 phép biến đổi sơ cấp….
  
  ThíchThích
  
  Posted by 2Bo02B | 11/03/2011, 22:58
  
  Reply to this comment

Bình luận về bài viết này Hủy trả lời

Đôi lời

Bạn có thể theo dõi các lời bình liên quan đến lời bình của mình qua email bằng cách chọn dòng thông báo Báo cho bạn khi có người bình luận tiếp theo đề tài này bằng điện thư mỗi khi viết 1 lời bình.

Rất mong các bạn viết lời nhắn bằng tiếng việt có dấu nhé.

Để viết tiếng việt có dấu bạn dùng font chữ Unicode và bảng mã là Unicode UTF-8.

Để biết cách gõ công thức Toán học trong các lời nhắn ở trang web này, mời bạn đọc bài hướng dẫn tại đây hoặc bạn có thể xem bài hướng dẫn dùng MathType tại đây và bài tạo công thức trực tuyến tại đây

	Dương Khánh Uyên trong Trang 2
	Trần Thái An trong Trang 2
	Chúc Chúc trong Xác suất có điều kiện
	Hoang Anh trong Khai triển Taylor – Macl…
	Trần Trung Đức trong Mẹo phân tích nhanh 1 phân…
	Nhung Duong trong Trang 2
	khoi trong Khai triển Taylor – Macl…
	Minh pham trong Chuỗi Fourier Sine và Cos…
	Minh Phạm trong Chuỗi Fourier
	Anh Tuấn trong Cực trị (không điều kiện) của…

Maths 4 Physics & more…

Tìm