Maths 4 Physics & more…
Shortlink: http://wp.me/P8gtr-MB
Phương trình cấp một tổng quát có dạng F(x,y,y’) = 0 (I)
Nếu giải ra được đối với y’ thì phương trình có thể viết dưới dạng:
hoặc:
hoặc:
Chú ý quan trọng:
– Thông thường, ta nên tìm cách biến đổi phương trình về dạng (1) và phân tích f(x,y) ở vế phải để biết dạng. Đa số, các phương trình đều có thể đưa được về 1 trong 6 dạng sau: phân ly biến số, đẳng cấp (thuần nhất), phương trình đưa về pt đẳng cấp được, pt tuyến tính, pt Bernoulli và pt vi phân toàn phần.
– Nếu từ (1) ta không đưa pt về 1 trong 6 dạng trên được thì thử nghịch đảo phương trình (2) đưa phương trình về dạng x là hàm số theo biến y. Nghĩa là: thì sẽ tìm được cách giải.
1. Bài toán cauchy (Bài toán điều kiện đầu):
Bài toán Cauchy là bài toán tìm nghiệm ptvp:
thỏa mãn điều kiện đầu:
Nghĩa là: tìm đường cong y = y(x) đi qua điểm (x0;y0) và thỏa mãn pt (1)
2. Định lý Peano – Cauchy – Picard (định lý tồn tại và duy nhất nghiệm):
Nếu hàm số f(x,y) liên tục trong miền mở
, thì với mọi điểm
, bài toán Cauchy (1), (2) có nghiệm xác định trong 1 lân cận của x0.
Ngoài ra, nếu đạo hàm riêng
cũng liên tục trong D thì nghiệm đó là duy nhất.
(ta công nhận định lý này, vì việc chứng minh vượt quá những kiến thức chúng ta được trang bị)
3. Nghiệm tổng quát:
Nghiệm tổng quát của pt (1) là hàm số , phụ thuộc biến x, và hằng số C, và thỏa mãn các điều kiện:
1. Nghiệm đúng ptvp với mọi giá trị cụ thể của C.
2. Với bất kỳ điều kiện đầu ta cũng có thể tìm được
sao cho hàm số
thỏa mãn điều kiện đầu
– Trong quá trình tìm nghiệm: nếu ta đi đến biểu thức (*) mà không giải được đối với y thì y là hàm ẩn theo x, C xác định bởi pt (*) và (*) được gọi là tích phân tổng quát.
– Các nghiệm của phương trình không suy ra được từ nghiệm tổng quát được gọi là nghiệm kỳ dị.
4. Phương trình phân ly biến số (tách biến)
Là phương trình có dạng:
(hoặc
)
Nghĩa là: ở vế phải ta gom được x đứng riêng và y đứng riêng (hoặc M(x) chỉ là hàm theo 1 biến số x và N(y) chỉ là hàm theo 1 biến số y)
4.1 Cách giải:
Ta biến đổi như sau:
Bằng cách lấy tích phân (vế trái theo y, vế phải theo x) ta được nghiệm tổng quát:
4.2 Ví dụ:
1. Giải phương trình:
Chuyển phương trình về dạng (1) ta có:
Vậy: x tách riêng, và y tách riêng nên đây là phương trình tách biến.
Khi đó ta có:
Ở đây do 2 vế đều có chứa ln nên thay vì ta chọn hằng số C thì ta chọn hằng số là lnC để dễ dàng rút gọn
Vậy nghiệm phương trình:
Hay:
2. Giải phương trình
Ta có: (phương trình tách biến)
Do đó:
Suy ra:
Bài này, ta cần xét thêm trường hợp tgy = 0.
3. Ví dụ tự giải:
4.3 Nhận xét:
Phương trình dạng
có thể đưa về phương trình tách biến bằng cách đổi qua ẩn hàm mới
Thật vậy, ta có:
Vậy vế phải là biểu thức chỉ phụ thuộc z. Nghĩa là z tách riêng và x tách riêng nên nó là phương trình tách biến.
5. Phương trình đẳng cấp:
– Hàm F(x,y) được gọi là hàm đẳng cấp bậc k nếu:
với mọi λ > 0, ta có:
– Ví dụ: Các hàm lần lượt là các hàm đẳng cấp bậc 0, bậc 1, bậc 3. Hàm
không là hàm đẳng cấp
5.1 Phương trình vi phân đẳng cấp: Phương trình được gọi là phương trình đẳng cấp nếu: f(x,y) là hàm đẳng cấp bậc 0, nghĩa là
– Lưu ý: một số giáo trình gọi tên dạng phương trình này là phương trình thuần nhất
– Nhận xét: Giả sử thì để (1) là phương trình đẳng cấp thì tất cả mọi số hạng có trong M(x,y) và N(x,y) phải cùng bậc.
– Ví dụ: phương trình: là phương trình đẳng cấp vì các số hạng đều là bậc 2. Phương trình:
là phương trình đẳng cấp vì
đều là các số hạng bậc 1.
5.2 Cách giải:
Theo định nghĩa pt đẳng cấp ta có: . Chọn
thì pt (1) có dạng:
(*)
Vế phải của pt (*) là 1 biểu thức luôn phụ thuộc y/x . Do vậy:
Đặt
Thế vào phương trình (5) ta có:
– Th1: Nếu
Khi đó:
Do đó pt (5) trở thành:
– Th2: Nếu
Khi đó: : pt tách biến.
5.3 Ví dụ: Giải phương trình vi phân:
Rõ ràng đây là phương trình đẳng cấp. Ta viết lại phương trình như sau:
Đặt: . Ta có:
, và thay vào phương trình ta có:
Lấy tích phân 2 vế ta được:
Hay:
Vậy nghiệm của phương trình có dạng:


Ad giúp e bài này với.xy’=y-xe^y/x tks trc ạ.
ThíchThích
Posted by Huy | 12/10/2016, 21:24Thay oi giai bai nay jum em 2ydx+(y^2-6x)dy=0
ThíchThích
Posted by ctkt chau | 23/06/2015, 22:21thầy ơi giải giúp em bài này xiu hen: giải pt: xsqrt(y^2+2xy+2x^2)dy =(2xy+3x^2)dy-(2y^2+3xy)dx điều kiện: y*(1+sqrt(2))=0 e cảm ơn thầy
ThíchThích
Posted by nguyễn thành hậu | 21/01/2015, 10:09thầy ơi giải giúp em bài này với ah (y+e^x)dx+xdy=0
ThíchThích
Posted by sue | 12/01/2015, 11:46thầy oi giup dùm e :phuong trinh tach biến :y’=x^2*y^2
ThíchThích
Posted by duyen doanthikim | 10/01/2015, 08:11thầy ơi giúp em bai nay ạ: xy’-2y=2. x^3
ThíchThích
Posted by Lục Bình | 15/07/2014, 09:56thầy ơi sao thầy không lấy thêm nhiều bài tập ví dụ nữa thầy? em thấy bài tập nó hơi ít ah!
ThíchThích
Posted by thanh lam | 26/11/2012, 20:40bên trên khi đặt x=u+h e nghĩ bên dưới la y=v+k chứ thầy
ThíchThích
Posted by Đỗ Khánh Duy | 10/06/2011, 03:06em thắc mắc tại sao ở vd 5.3 thầy không xét TH x=0 với x#0 ??????
Thầy có thể giải thích rõ tại sao không xét không
ThíchThích
Posted by Tuan Vu | 31/01/2011, 19:51thầy cho em hỏi bài giải phương trình vi phân :y’=x+y .cám ơn thầy ^^
ThíchThích
Posted by Lam Như | 23/10/2010, 22:06Thầy ơi, em bị bí bài này thầy giải giúp em với ạ: Xét PTVP (y^2-2xy)dx+(x^2-5xy)dy=0.
Khẳng định nào sau đây dúng:
1.PTVP dẳng cấp
2. PTVP Bernoulli
3.PTVP tách biến
4.PTVI tuyến tính
ThíchThích
Posted by Mộng Tuyền | 18/09/2010, 09:45Để tìm dạng ptvp, em cứ biến đổi về dạng: . Sau đó, phân tích f(x,y) để tìm ra dạng của nó.
. Sau đó, phân tích f(x,y) để tìm ra dạng của nó.
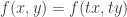 . Vậy nó là dạng pt gì chắc em đã nhận ra.
. Vậy nó là dạng pt gì chắc em đã nhận ra.
Ở đây, em có
Tất cả số hạng ở vế phải đều có bậc là 2 nên
ThíchThích
Posted by 2Bo02B | 18/09/2010, 10:12