Maths 4 Physics & more…
Ta đã biết rằng khái niệm đạo hàm riêng cho chúng ta biết được tốc độ thay đổi của hàm số khi cho 1 trong các biến số thay đổi giá trị. Bây gờ, chúng ta sẽ nghiên cứu sự thay đổi của hàm số 2 biến khi cho cả hai biến số thay đổi.
Xét hàm số và
là điểm thuộc miền xác định D. Ta cho x, y thay đổi 1 lượng tương ứng
sao cho
. Khi đó, giá trị của hàm số sẽ thay đổi một lượng:
1. Định nghĩa 1:
Hàm số f(x;y) được gọi là khả vi tại điểm
nếu số gia toàn phần
có thể biểu diễn được dưới dạng:
(1)
trong đó A, B là những số không phụ thuộc Δx, Δy; còn α, β → 0 khi Δx, Δy → 0
Khi đó, đại lượng A.Δx +B.Δy được gọi là vi phân toàn phần của hàm số f(x;y) tại
ứng với các số gia Δx, Δy và được ký hiệu
Ví dụ:
Xét hàm số . Ta có:
Hay:
Do đó:
Cho nên hàm số khả vi tại và
Nhận xét:
1. Xét ,
Cho thì
. Khi đó, áp dụng bất đẳng thức B.C.S và giới hạn kẹp ta có:
Do đó, ε là VCB khi ρ → 0.
Vì vậy, biểu thức (1) có thể viết dưới dạng:
, 0(ρ) là vô cùng bé bậc cao hơn ρ.
2. Ta không thể dùng định nghĩa để xét sự khả vi của hàm số như ở ví dụ 1 được. Tổng quát, chỉ có thể áp dụng định nghĩa để xét sự khả vi cho những hàm số dạng đa thức, còn các hàm số khác thì không thể dùng định nghĩa để khảo sát sự khả vi tại 1 điểm. Vì vậy, ta cần phải tìm một công cụ khác để giải quyết vấn đề này.
3. Hàm số được gọi là khả vi trên miền D nếu nó khả vi tại mọi điểm thuộc D.
2. Định lý 1: (Điều kiện cần để hàm số khả vi)
Nếu hàm số
khả vi tại
thì nó liên tục tại điểm đó.
Chứng minh:
Vì hàm số khả vi, nên từ công thức (1) ta có:
Vậy:
Do đó, hàm số liên tục tại .♦
Nhận xét:
1. Nếu hàm số f(x;y) không liên tục tại thì sẽ không khả vi tại điểm đó.
2. Hàm số khả vi trên miền D thì liên tục trong miền đó.
3. Định lý 2:
Nếu f(x;y) khả vi tại
thì nó có các đạo hàm riêng
tại
và chúng tương ứng bằng A và B trong biểu thức 1 của định nghĩa hàm số khả vi.
Chứng minh:
Thật vậy, từ công thức (1) ta cho , ta được:
trong đó α →0 khi Δx → 0.
Do đó:
Vậy
Hoàn toàn tương tự ta có:
Nhận xét:
1. Như vậy, nếu hàm số f(x,y) khả vi tại thì vi phân toàn phần của hàm số tại
được xác định bởi:
2. Khác với hàm số 1 biến (nếu hàm số có đạo hàm thì sẽ khả vi), nếu hàm số hai biến số f(x,y) có các đạo hàm riêng tại $latex(x_0;y_0) thì chưa chắc nó đã khả vi tại điểm đó. Ta xét hàm số sau:
Theo định nghĩa đạo hàm riêng, ta có:
Tương tự ta có: nhưng hàm số G(x;y) không liên tục tại (0; 0) (xem phần giới hạn hàm nhiều biến) nên không khả vi tại (0;0)
4. Định lý 3 (Điều kiện đủ để hàm số khả vi)
Cho hàm số f(x;y) có các đạo hàm riêng trong một miền D chứa điểm
. Nếu các đạo hàm riêng ấy liên tục tại M thì hàm số khả vi tại điểm đó.
5. Các ví dụ:
1. Cho hàm:
Tính và
. Hàm có khả vi tại (0;0) hay không?
Giải
Để tính các đạo hàm riêng tại (0;0) ta phải dùng định nghĩa mà không thể thế giá trị (0;0) vào biểu thức đạo hàm
Ta có:
tương tự: =
=
Mặc dù, hàm số có 2 đạo hàm riêng tại (0;0) nhưng không khả vi tại điểm đó vì hàm số đã cho không liên tục tại (0;0). Thật vậy: xét điểm (x;y) tiến về điểm (0;0) theo đường thẳng y = kx ta có.
Vậy giá trị giới hạn phụ thuộc vào hệ số k nện giới hạn không tồn tại.
Do đó:
Nên hàm số không liên tục tại (0;0) và do đó nó không khả vi tại (0;0)
2. Tìm vi phân của hàm số:
Hàm số luôn xác định và liên tục với mọi nên khả vi tại mọi điểm
. Khi đó ta có:


em thua thay thay giup em bai voi ak
tim a b de
[axcos(x^2+3y^2)+2.3^^(2x-y)]dx+[6ycos(x^2+3y^2)+b.3^^(2x-y)]dy la vi phan toan phan cua 1 ham U(x,y) nao do
ThíchThích
Posted by nguyen chien thang | 28/05/2012, 01:25thầy giải giúp em bài này với ạ.
Xét tính khả vi của hám số:
F(x,y) = (xy)/căn của (x^2+y^2) nếu (x,y) # 0
0 nếu (x,y) = 0
Em cảm ơn thầy!
ThíchĐã thích bởi 1 người
Posted by tuấn | 30/12/2011, 15:30Thầy ơi, hướng dẫn giúp em bài này với:
Tìm tốc độ thay đổi cùa hàm f(x,y,z)= x^2-y+z tại điểm (1,1,1) theo hướng vuông góc với mặt X^2 +y^2 -z =1 tại điểm (1,-1,1)
em cảm ơn thầy!!
ThíchThích
Posted by Minh Thanh | 14/12/2011, 10:54thưa thầy em mong thầy cho em phương pháp cụ thể để chứng minh hàm số khả vi.em cảm ơn thầy rất nhiều
ThíchThích
Posted by phạm thu | 24/11/2011, 05:09em thưa thầy vậy muốn kết luận hàm số có khả vi không thì bước một là minh phải chứng minh hàm số đó có đaoh hàm riêng và đạo hàm riêng tại mọi (x,y) # (o, o). sau đó mới đến điểm (o,o) ạ?. ( điểm (o,o) là điểm mà đầu bài cho sẵn)
ThíchThích
Posted by choxinh | 22/05/2011, 23:00Thầy giúp giùm em bài này :
Tìm a để hàm số f(x) =sinx – ax/x^2 (x#0) khả vi tại x=0
f(x) = 0 (x=0)
ThíchThích
Posted by ox_ngo | 18/01/2011, 08:08với cách giải của thầy ứng dụng vói hàm 2 biến,mở rộng với hàm n biến, xét tính khả vi có làm tương tự không ạ?thầy có thể cho em một vd minh họa không ạ?em cảm ơn thầy nhìu
ThíchThích
Posted by dao thi loan | 13/01/2011, 11:45Sự khả vi của hàm 2 biến khác với sự khả vi của hàm 1 biến. Nhưng sự khả vi của hàm nhiều biến thì hoàn toàn tương tự nhau. Do đó, em có thể mở rộng với hàm n biến.
ThíchThích
Posted by 2Bo02B | 13/01/2011, 21:24thầy ơi biểu thức này từ đâu có vậy thày em ko hiểu
f(x0+h)-f(x0)=f'(x0).h + a.h
ThíchThích
Posted by Nguyen thanh canh | 26/10/2010, 08:46thầy ơi em ko biết câu này thầy chỉ hướng cho em với:
cho ham số f:[a,b], chứng minh nếu f khả vi tại x0 thì liên tục tại x0
thay oi giúp em voi, em cám ơn thầy nhiều
ThíchThích
Posted by Nguyen thanh canh | 21/10/2010, 19:56Em sử dụng định nghĩa về hàm số khả vi tại x0, em sẽ có:
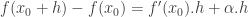 , với
, với  khi
khi 
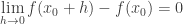

Từ điều trên, em dễ dàng có được:
Hay:
Điều này, chứng tỏ f liên tục tại x0.
ThíchThích
Posted by 2Bo02B | 21/10/2010, 21:26thầy giúp em giải bài này
tìm vi phân toàn phần: z=(x2+x+xy)ngũ(x-y+1)
em cảm ơn thầy
ThíchThích
Posted by phu | 03/06/2010, 21:56Cảm ơn thầy. Em đã tìm được câu trả lời cho mình (by counter-evidence method).
ThíchThích
Posted by Duc Lam | 29/05/2010, 10:39