Đạo hàm và vi phân của hàm số (derivative and differential of a function)

I. Đạo hàm (derivative)

1. Định nghĩa đạo hàm:

Cho hàm số $y = f(x)$ xác định trên D, $x_0 \in D$ .

Cho $x_0$ số gia ${\Delta}x$ (không phân biệt dương hay âm) sao cho: $x_0 +{\Delta}x \in D$ . Ta gọi ${\Delta}y = f(x_0+{\Delta}x) - f(x_0)$ là số gia của hàm số $y = f(x)$ .

Lập tỷ số:

$\dfrac{{\Delta}y}{{\Delta}x} = \dfrac{f(x_0+{\Delta}x)-f(x_0)}{{\Delta}x}$

Tìm giới hạn của tỉ số trên khi ${\Delta}x$ . Khi đó, giới hạn hữu hạn (nếu có) được gọi là đạo hàm của hàm số tại $x_0$ và ký hiệu $f'(x_0)$

Như vậy: $f'(x_0) = \lim\limits_{{\Delta}x \to 0} \dfrac{f(x_0+{\Delta}x)-f(x_0)}{{\Delta}x}$

Nếu đặt $x = x_0 +{\Delta}x$ , ta có: $f'(x_0) = \lim\limits_{x \to x_0} \dfrac{f(x)-f(x_0)}{x-x_0}$

Tổng quát: $f'(x) = \lim\limits_{{\Delta}x \to 0} \dfrac{f(x+{\Delta}x)-f(x)}{{\Delta}x}$

– Đạo hàm trái: nếu giới hạn $\lim\limits_{{\Delta}x \to 0-} \dfrac{f(x_0+{\Delta}x)-f(x_0)}{{\Delta}x}$ tồn tại và hữu hạn thì giới hạn đó gọi là đạo hàm bên trái của f(x) tại $x_0$ . Ký hiệu $f_{-}^{'}(x_0)$

– Đạo hàm phải: nếu giới hạn $\lim\limits_{{\Delta}x \to 0+} \dfrac{{\Delta}y}{{\Delta}x}$ tồn tại và hữu hạn thì giới hạn đó gọi là đạo hàm bên phải của f(x) tại $x_0$ . Ký hiệu $f_{+}^{'}(x_0)$

– Từ tính chất của giới hạn ta có định lý sau:

Hàm số f(x) có đạo hàm tại $x_0$ khi và chỉ khi f(x) có đạo hàm trái và đạo hàm phải tại $x_0$ và các đạo hàm đó bằng nhau.

Ví dụ 1: Cho hàm số: $f(x) = \left\{\begin{array}{cl} x & ; x \le 1 \\ -x^2+2x & ; x \rm{>} 1 \\ \end{array} \right.$

Tìm $f'(1)$

Ta có:

$f_{+}^{'}(1) = \lim\limits_{x \to 1+} \dfrac{f(x)-f(1)}{x-1} = \lim\limits_{x \to 1+} \dfrac{-x^2+2x-1}{x-1} = 0$

$f_{-}^{'}(1) = \lim\limits_{x \to 1-} \dfrac{f(x)-f(1)}{x-1} = \lim\limits_{x \to 1-} \dfrac{x-1}{x-1} = 1$

Vậy $f_{+}^{'}(1) \ne f_{-}^{'}(1)$

Do đó: f(x) không có đạo hàm tại x = 1.

2. Ý nghĩa hình học của đạo hàm

3. Các định lý về đạo hàm:

3.1 Định lý 1: Nếu hàm số f(x) có đạo hàm tại $x_0$ thì f(x) liên tục tại điểm đó. (Chiều ngược lại chưa chắc đúng).

Chứng minh: do f(x) có đạo hàm tại $x_0$ nên:

$\lim\limits_{{\Delta}x \to 0} \dfrac{{\Delta}y}{{\Delta}x} = f'(x_0)$

Theo định nghĩa giới hạn, ta có $\dfrac{{\Delta}y}{{\Delta}x} = f'(x_0) + \epsilon$ ( $\epsilon \rm{<<}$ )

Từ đó: ${\Delta}y = f'(x_0).{\Delta}x + {\epsilon}.{\Delta}x$

Do $\epsilon \rm{<<} , \epsilon \to 0$ nên: ${\epsilon}.{\Delta}x$ là VCB cấp cao hơn ${\Delta}x$ khi ${\Delta}x \to 0$

Vì vậy: $\lim\limits_{{\Delta}x \to 0} {\Delta}y = 0$

Nghĩa là: $\lim\limits_{{\Delta}x \to 0} f(x_0+{\Delta}x) - f(x_0) = 0$

Hay: $\lim\limits_{x \to x_0} f(x) = f(x_0)$

Vậy: f(x) liên tục tại $x_0$

– Chiều ngược lại không chắc đúng: ta xét lại ví dụ 1 ở trên. Rõ ràng, hàm f(x) liên tục tại x = 1 nhưng không có đạo hàm tại điểm đó.

– Phản ví dụ 2: Xét hàm số $f(x) = |x|$ liên tục trên R nhưng không có đạo hàm tại x = 0.

3.2 Định lý 2: (quy tắc tính đạo hàm)

Nếu u(x) và v(x) là các hàm có đạo hàm tại x thì tổng, hiệu, tích thương cũng có đạo hàm tại x và ta có các công thức:

1. $(u \pm v)' = u' \pm v'$

2. $(u.v)' = u'.v + v'.u$

3. $\left( \dfrac{u}{v} \right)^{'} = \dfrac{u'.v-v'.u}{v^2}$

3.3 Định lý 3: (đạo hảm hàm số hợp)

Nếu $y = f(x)$ có đạo hàm tại $x_0$ và $z = g(y)$ xác định trong một khoảng chứa $y_0 = f(x_0)$ và có đạo hàm tại $y_0$ . Khi đó: hàm $z = g(f(x))$ có đạo hàm tại $x_0$ và

$z'(x_0) = g'(y_0).f'(x_0) (3.3)$

Tổng quát: $z_x^{'} = z_{y}^{'}.y_{x}^{'}$

Chứng minh:

Ta có: $\lim\limits_{{\Delta}y \to 0}\dfrac{{\Delta}z}{{\Delta}y} = z_y^{'}(y_0)$

Từ định nghĩa giới hạn, ta suy ra: $\dfrac{{\Delta}z}{{\Delta}x} = z_y^{'}(y_0) + \alpha$ (1)

trong đó $\alpha \to 0$ khi ${\Delta}y \to 0$

Viết lại đẳng thức (*) ta có: ${\Delta}z = z_y^{'}(y_0).{\Delta}y + {\alpha}.{\Delta}y$ (2)

Chia 2 vế của (3) cho ${\Delta}x$ ta có:

$\dfrac{{\Delta}z}{{\Delta}x} = z_y^{'}(y_0).{\dfrac{{\Delta}y}{{\Delta}x}} +{\alpha} \dfrac{{\Delta}y}{{\Delta}x}$

Mặt khác, do : ${\Delta}y = f(x_0+{\Delta}x) - f(x_0)$ nên ${\Delta}x \to x$ thì ${\Delta}y \to 0$

Vậy: $\lim\limits_{{\Delta}x \to 0} \alpha = 0$ (4)

Mà: $\lim\limits_{{\Delta}x \to 0} \dfrac{{\Delta}y}{{\Delta}x} = y_x^{'}(x_0)$ (5)

Do đó: từ (3), (4), (5) ta có:

$\lim\limits_{{\Delta}x \to 0} \dfrac{{\Delta}z}{{\Delta}x} = z_y^{'}(x_0).y_x^{'}(x_0)$ .

3.4 Định lý 4: (đạo hàm hàm số ngược)

Cho hàm số y = f(x) liên tục và đồng biến (hoặc nghịch biến) trong khoảng (a,b). Nếu f(x) có đạo hàm tại $x_0 \in (a,b)$ và $f'(x_0) \ne 0$ thì hàm ngược $x = g(y)$ của f(x) cũng có đạo hàm tại $y_0 = f(x_0)$ và:

$g_y^{'}(y_0) = \dfrac{1}{f_x^{'}(x_0)} (3.4)$

Chứng minh:

Vì f(x) là hàm đồng biến (nghịch biến) trong khoảng (a,b) nên tồn tại duy nhất hàm ngược $x = g(y)$

Khi đó, xét: $\dfrac{g(y)-g(y_0)}{y-y_0} = \dfrac{x - x_0}{f(x) - f(x_0)} = \dfrac{1}{\dfrac{f(x) - f(x_0)}{x - x_0}}$ (*)

Cho $x \to x_0$ . do f(x) là hàm liên tục nên: $f(x) \to f(x_0)$ , hay $y \to y_o$

Lấy giới hạn của (*) khi $y \to y_0$ . ta có:

$g_y^{'}(y_0) = \dfrac{1}{f_x^{'}(x_0)}$ (dpcm)

Ví dụ 1: Cho $y = arcsinx$ Tính $y_x^{'}$

Ta có: $y = arcsinx \Rightarrow x = siny$

Theo công thức (3.4), ta có: $y_x^{'} = \dfrac{1}{x_y^{'}} = \dfrac{1}{cosy}$

Mà do $y = arcsinx \Rightarrow y \in \left[ -\dfrac{\pi}{2},\dfrac{\pi}{2} \right] \Rightarrow cosy \ge 0$

Nên: $cosy = \sqrt{1-sin^2y} = \sqrt{1-x^2}$

Do đó:

$(arcsinx)' = \dfrac{1}{\sqrt{1-x^2}} (-1 \rm{<} x \rm{<} 1 )$

Ví dụ 2: Cho $y = arccosx$ . Tìm $y_x^{'}$

Ta có: $y = arccosx \Rightarrow x = cosy$

Nên: $y_x^{'} = \dfrac{1}{x_y^{'}} = \dfrac{1}{-siny} = \dfrac{-1}{siny}$

Lại có: $y = arccosx \Rightarrow y \in [0,\pi] \Rightarrow siny \ge 0$

Suy ra: $y_x^{'} = \dfrac{-1}{siny} = \dfrac{-1}{\sqrt{1-cos^2y}} = \dfrac{-1}{\sqrt{1-x^2}}$

Vậy:

$(arccox)' = \dfrac{-1}{\sqrt{1-x^2}} (-1 \rm{<} x \rm{<} 1 )$

Ví dụ 3: Cho $y = arctanx$ . Tính $y_x^{'}$

tương tự: $y = arctanx \Rightarrow x = tany$

Suy ra: $y_x^{'} = \dfrac{1}{x_y^{'}} = \dfrac{1}{1+tan^2y} = \dfrac{1}{1+x^2}$

Vậy:

$(arctanx)' = \dfrac{1}{1+x^2}$

Ví dụ 4: Cho $y = (arcsinx)^{arctanx} \left( 0 \rm{<} x \le 1 \right)$ . Tìm y’?

Ta có: $y = e^{(arctanx).ln(arcsinx)} \Rightarrow y' = e^{(arctanx).ln(arcsinx)}.((arctanx).ln(arcsinx))'$

Lại có: $((arctanx).ln(arcsinx))' = \dfrac{ln(arcsinx)}{1+x^2} + \dfrac{arctanx}{(arcsinx).\sqrt{1-x^2}}$

Vậy: $y' = e^{(arctanx)ln(arcsinx)}. \left[ \dfrac{ln(arcsinx)}{1+x^2} + \dfrac{arctanx}{(arcsinx).\sqrt{1-x^2}} \right] (\rm{0 < x < 1})$

(còn tiếp)

Thảo luận

13 bình luận về “Đạo hàm và vi phân của hàm số (derivative and differential of a function)”

em chao thay,thay cho em hoi muon giai bai nay phai lam the nao a
I=lim(1+x binh)mu cotg binh x {khi x dan den 0}.voi dap so la(I=e).em mong thay huong dan cho em voi a.em cam on thay nhieu……..

ThíchThích

Posted by tuyet | 29/09/2012, 11:40

Reply to this comment
thầy ơi, cho em hỏi cách tìm y’,biết y= arcsecx

ThíchThích

Posted by tuankiet | 19/01/2012, 11:18

Reply to this comment
em cung da can chung minh giong ban tren vay thua thay:
” em muốn hỏi nếu 2 hàm số không có đạo hàm tại x0 thì có thể khẳng định tổng của nó không có đạo hàm tại x0 không thầy?
Hoặc nếu chỉ một trong 2 hàm f và g có đạo hàm tại x0 cũng hỏi tương tự luôn thì có đúng không? Mong thầy giúp em.”
giup em voi .em dang lam de tai tieu luan toan dai cuong a1

ThíchThích

Posted by chanh | 26/11/2011, 20:50

Reply to this comment
thay oi, cho em hoi! vi phan va dao ham giong va khac nhau o cho nao?

ThíchThích

Posted by nguyenduyhien | 24/11/2011, 11:17

Reply to this comment
Thầy ơi cho em hỏi nếu cho hàm số dạng phân đoạn với x lớn hơn 0 và x nhỏ hơn hoặc bằng 0. Nếu bài yêu cầu tìm a, b để hàm số có đạo hàm thì mình chỉ cần cho đạo hàm trái bằng đạo hàm phải, hay phải thêm điều kiện liên tục nữa.

ThíchThích

Posted by Thảo Lý | 31/10/2011, 21:13

Reply to this comment
- Nếu đề bài yêu cầu là có đạo hàm tại x =0: thì chỉ cần đạo hàm trái bằng đạo hàm phải (tại x = 0).
  Nếu đề bài yêu cầu có đạo hàm liên tục tại x = 0 thì phải có đk hàm có đạo hàm tại x = 0 và hàm đạo hàm f'(x) liên tục tại x = 0.
  Nếu đề bài yêu cầu có đạo hàm gián đoạn thì chứng minh có đạo hàm nhưng hàm đạo hàm f'(x) không liên tục.
  
  ThíchThích
  
  Posted by 2Bo02B | 02/11/2011, 08:43
  
  Reply to this comment
thầy ơi, cho em hỏi bài này ạ:
Cho g(x) liên tục và ko có đạo hàm tại x0. Chứng minh rằng tồn tại vô số f(x) sao cho f(x).g(x) có đạo hàm tại x0?

ThíchThích

Posted by Thuy Dung | 24/06/2011, 11:17

Reply to this comment
Thầy cho em hỏi: muốn giải hàm này thì làm cách nào ạ?
y=2cos^4.x-sin^4.x+sin^2.x.cos^2.x+3sin^2.x có đạo hàm bằng 0.

ThíchThích

Posted by thuy | 01/04/2011, 08:58

Reply to this comment
- Em có thể lấy đạo hàm, rồi sử dụng các tính chất của hàm lượng giác để chứng minh. Tuy nhiên, ở đây, đề bài yêu cầu chứng minh bểu thức có đạo hàm bằng 0, có nghĩa hàm số đã cho phải là hàm hằng. Từ chú ý đó, ta có thể biến đổi biểu thức trước khi lấy đạo hàm. Em chú ý số hạng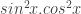 $sin^2x.cos^2x$ , ta có thể chuyển về theo lũy thừa của sin hoặc của cos. Khi đó:
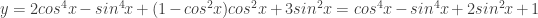
  $y = 2cos^4x -sin^4x + (1-cos^2x)cos^2x + 3 sin^2x = cos^4x - sin^4x + 2sin^2x + 1$
  Em chú ý thêm chút xíu sẽ có kết quả $y = 2$
  
  ThíchThích
  
  Posted by 2Bo02B | 03/04/2011, 22:43
  
  Reply to this comment
  - em cam ơn thầy.à mà nếu lần sau em có câu muốn hỏi thì em có thể hỏi th dc ko a?
    
    ThíchThích
    
    Posted by thuy | 05/04/2011, 08:41
    
    Reply to this comment
em cam on thay nhieu

ThíchThích

Posted by kim phuong | 24/12/2010, 10:26

Reply to this comment
Thầy ơi, em muốn hỏi nếu 2 hàm số không có đạo hàm tại x0 thì có thể khẳng định tổng của nó không có đạo hàm tại x0 không thầy?
Hoặc nếu chỉ một trong 2 hàm f và g có đạo hàm tại x0 cũng hỏi tương tự luôn thì có đúng không? Mong thầy giúp em.

ThíchThích

Posted by kim phuong | 18/12/2010, 15:48

Reply to this comment
- Em có phản ví dụ sau: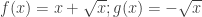
  Hàm $f(x) = x + \sqrt{x} ; g(x) = -\sqrt{x}$ là hai hàm không có đạo hàm tại 0; nhưng 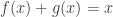$f(x) + g(x) = x$ lại là hàm có đạo hàm tại x =0.
  
  ThíchThích
  
  Posted by 2Bo02B | 20/12/2010, 14:10
  
  Reply to this comment

Bình luận về bài viết này Hủy trả lời

Đôi lời

Bạn có thể theo dõi các lời bình liên quan đến lời bình của mình qua email bằng cách chọn dòng thông báo Báo cho bạn khi có người bình luận tiếp theo đề tài này bằng điện thư mỗi khi viết 1 lời bình.

Rất mong các bạn viết lời nhắn bằng tiếng việt có dấu nhé.

Để viết tiếng việt có dấu bạn dùng font chữ Unicode và bảng mã là Unicode UTF-8.

Để biết cách gõ công thức Toán học trong các lời nhắn ở trang web này, mời bạn đọc bài hướng dẫn tại đây hoặc bạn có thể xem bài hướng dẫn dùng MathType tại đây và bài tạo công thức trực tuyến tại đây

	Dương Khánh Uyên trong Trang 2
	Trần Thái An trong Trang 2
	Chúc Chúc trong Xác suất có điều kiện
	Hoang Anh trong Khai triển Taylor – Macl…
	Trần Trung Đức trong Mẹo phân tích nhanh 1 phân…
	Nhung Duong trong Trang 2
	khoi trong Khai triển Taylor – Macl…
	Minh pham trong Chuỗi Fourier Sine và Cos…
	Minh Phạm trong Chuỗi Fourier
	Anh Tuấn trong Cực trị (không điều kiện) của…

Maths 4 Physics & more…

Tìm

Thảo luận

13 bình luận về “Đạo hàm và vi phân của hàm số (derivative and differential of a function)”

Bình luận về bài viết này Hủy trả lời

Translators & RSS

Đăng ký nhận tin

Đôi lời

Lời nhắn mới nhất

Bài “hot”

Bài viết chuyên đề

Maths 4 Physics & more…

Tìm

Đánh giá:

Chia sẻ:

Thảo luận

13 bình luận về “Đạo hàm và vi phân của hàm số (derivative and differential of a function)”

Bình luận về bài viết này Hủy trả lời

Translators & RSS

Đăng ký nhận tin

Đôi lời

Lời nhắn mới nhất

Bài “hot”

Bài viết chuyên đề